Recently, for a graduated mobile robotics class, I had to present a scientific paper. Loving algorithms, I decided to read Matching with PROSAC - Progressive Sample Concensus1, a paper presenting a variant of the popular RANSAC algorithm.
This article will be a more detailed version of the presentation I gave for that class, the slides are here. I won’t go into much of the mathematics, the details are in the paper. What I want to do with this article is to give you the intuition behind the algorithm more than writing a lot of equations.
To supplement the presentation, I wrote an implementation of PROSAC in Python: willGuimont/PROSAC.
Before jumping in PROSAC, let’s just review RANSAC a bit.
RANSAC - Random sample consensus
The main goal of RANSAC is to estimate a model from noised data with outliers.
The basic idea is to randomly sample points from all points; fit a model on those randomly chosen points; then check if the model fits with the rest of the data.
As you can see, the algorithm is relatively simple: sample, fit, check, rinse and repeat.
Pseudocode
Let \(m\) be the minimum required number of points to fit a model. For a linear model in 2D, \(m\) would be equal to \(2\).
Let \(M\) a model to fit on the data.
Let \(\epsilon_{tol}\) be the maximum error between a point and the model to be considered an inlier.
Let \(\tau\) the fraction of inlier over the total number of points above which we are satisfied by the model. If we achieve that ratio, we stop early.
Let \(w\) be the probability of a given point to be an inlier. This is used to estimate the number of times we have to run RANSAC before finding a satisfying solution.
Let \(I\) be the set of inliers of maximal cardinality.
RANSAC
- Sample \(m\) points
- Estimate a model \(M\) from the \(m\) sampled points
- Find the number of inliers with model \(M\) with tolerance \(\epsilon_{tol}\). If the number of inliers is greater than the number of previously found inliers, replace \(I\) with the new set of inliers.
- If the fraction of inliers over the total number of points is greater than \(\tau\), estimate the model with all inliers and stop.
- Repeat steps 1 to 4, a maximum of \(\frac{1}{w^m}\) times
- After \(\frac{1}{w^m}\) iterations, estimate the model with \(I\).
Limitations of RANSAC
In the paper, they looked at estimating epipolar geometry from a pair of pictures.
 |
 |
With this pair of pictures, there is a lot of repetitive patterns on the floor and leaves, so there will be a lot of false matches. We have \(m=7\) (epipolar geometry) and \(w=9.2\%\). The number of iteration of RANSAC is given by \(\frac{1}{w^m}\). The estimated number of samples is over \(8.43 \times 10^7\) !!! RANSAC would take a pretty long time before finding a good solution… That’s not realistic!
When the model is complex and the number of correct points is low, RANSAC often takes very long before finding a satisfying solution. Let’s see if PROSAC can help.
PROSAC - Progressive sample consensus
PROSAC adds the notion of quality to points with the basic assumption that points of greater quality have more chances to be correct.
So, to make the algorithm quicker, the algorithm starts by trying to fit with points of greater quality first. Then we progressively add points of lesser quality.
Intuition
Let’s say that the points in red are outliers. We would like to fit a model of complexity \(m=2\) on those points.
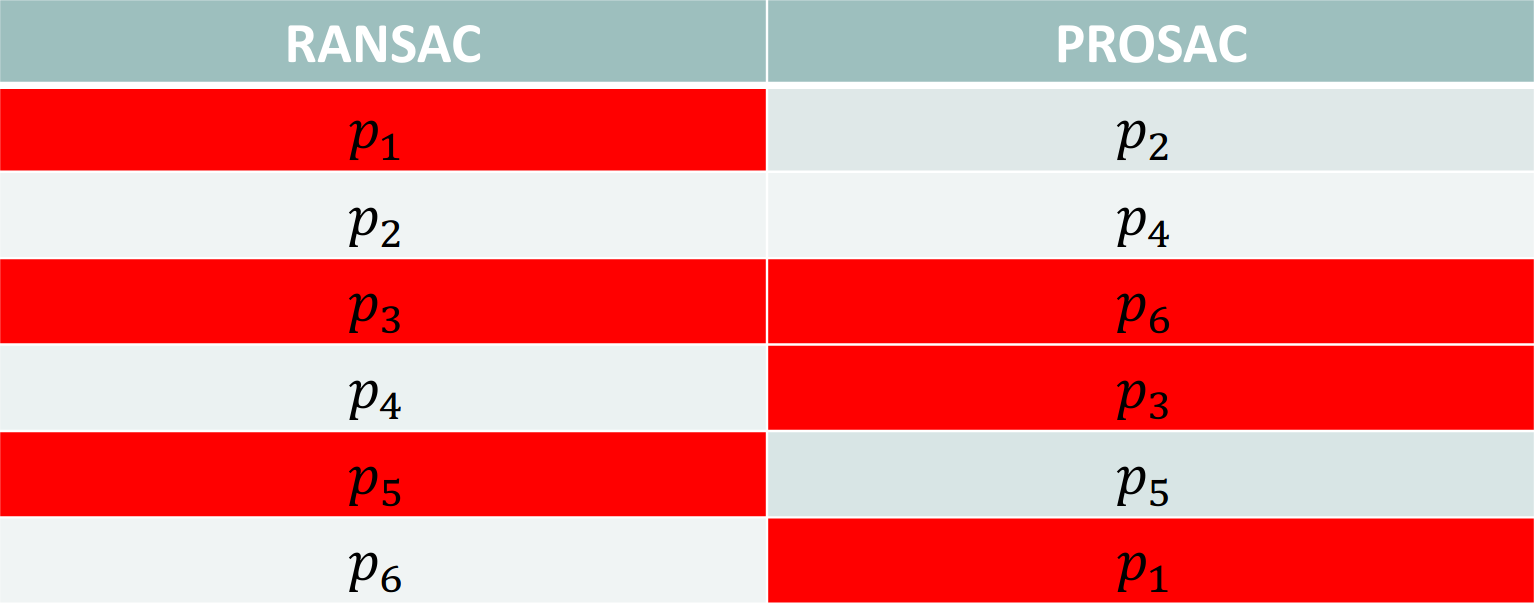
In RANSAC, we would be sampling \(2\) points among all points, so we would have a probability of \(\frac{3}{6}\cdot\frac{2}{5}=20\%\). So, we would need, on average, \(5\) samples before finding an uncontaminated sample.
Whereas in PROSAC, we sort points by quality. The first points would be of higher quality. We would start sampling from the top 2 points, so we would sample \(p_2\) and \(p_4\), both of which are correct. In this case, we would have found an uncontaminated sample on the first draw.
Even with this simple example, we can see the possible speedup.
Simplified pseudo code
PROSAC
- Sort points by quality (highest quality first)
- Consider the first \(m\) points (\(n\leftarrow m\))
- Sample \(m\) points from the top \(n\)
- Fit the model
- Verify model with all points
- If the stopping criteria are not met, repeat steps 3 to 6, adding progressively points (\(n\leftarrow n + 1\)). Otherwise, fit the model on all inliers and terminate.
Quality
There are multiple ways of defining quality. For feature matching on images, we could use the correlation of intensity around features on each image.
In the paper, they mention Lowe’s distance. Lowe’s distance is the ratio between the most and second most similar matches.
\(s_1\): distance of the most similar match
\(s_2\): distance of the second most similar match
\[distance = \frac{s_1}{s_2}\]This distance allows us to select the first points that are significantly better than any other. A match with a low Lowe’s distance has more chances of being correct.
To define quality, we could inverse the ratio.
\[quality = \frac{s_2}{s_1}\]You can use any metric you want, as long as the higher the quality is, the higher the probability of the point being correct is.
Fast sampling
We could simply sample \(m\) points from the top \(n\) points, but that would be inefficient. We could sample multiple times the same set of points. So, to better explore the new possibles sets of \(m\) points, we use the fact that when adding a new point \(p_{n+1}\), we add a number \(a\) of new samples. Each new sample contains the new point \(p_{n+1}\) and \(m-1\) from the \(n\) first points.
So, we can simply sample \(a\) times, picking \(p_{n+1}\) and \(m-1\) points in the best \(n\) points. That way, we ensure the quickly explore the possibles sets of \(m\) points.
End criterion
The algorithm has two stopping criteria.
- Non-random solution
- Maximality
Non-random solution
This criterion states that for a solution to be considered correct, it must have more inliers than what would randomly happen for an incorrect model.
This is computed by estimating the probability that an incorrect model (fitted on a sample) is supported by a given point, not in the sample.
The solution is considered non-random if the probability of having its number of inliers by chance is smaller than a certain threshold (usually 5%).
Maximality
We want to stop sampling when the chance of getting a model that fit more points is lower than a certain threshold. This is computed by looking at the odds of missing a set of inliers bigger than previously found after a number of draws. If this probability falls under a certain threshold (usually 5%), it is not worth continuing drawing and we terminate.
Code
Not having found any implementation of PROSAC online, I decided to post mine: willGuimont/PROSAC.
Sources
-
Chum, Ondrej & Matas, Jiri. Matching with PROSAC - Progressive Sample Consensus. 2005. ↩