In my third session of CÉGEP, I decided to take a thermodynamic and astrophysics class. It was the kind of class that completely changed the way you see physics.

I have always seen physics experiments as things you just cannot do at home. You always need some complicated apparatus. Yet, in this class, we calculated the eccentricity of the Moon’s orbit, a bit of rock spinning around Earth, using only a camera and a bit of imagination.

The idea is quite simple, as the Moon moves closer and further of the Earth, its visual size will vary. When the Moon is at its perigee (closest to the Earth), it will appear bigger than when the Moon is at its apogee (further from the Earth). If we can measure its visual size around its orbit, we could deduce the orbit’s eccentricity.

So, to get that data we took pictures of the Moon and measure its diameter in the pictures. If we use the same camera and don’t modify the focal length of the lens, the only thing that will make vary the Moon’s size in the picture will be the distance from Moon to Earth.

Here is some pictures I took back then:

In each picture, we can measure the Moon’s diameter in pixel.

We can then compute the distance between Earth and the Moon and pixel in each picture using:

\[d=\frac{r}{tan \left (\frac{0.5°}{2} \right )}\]

Where \(r\) is the radius, in pixel, of the Moon in the picture. Notice that \(0.5°\) is the angular size of the Moon from Earth. To understand this equation, try to draw a right triangle from the Earth to the Moon.

Using the date at which the photo was taken, we can compute its angular position relative to other photos. This can be done knowing that the Moon moves 360° around the Earth in 29.5 days on average. Assuming the Moon’s speed does not change on its orbit, we can compute it’s angle using:

\[\theta_i = (D_i - D_1) \cdot \frac{360°}{29.5} \bmod 360°\]

Where \(D_i\) if the current picture, \(D_1\) is the first picture (all positions will be relative to this one). Both dates are in days.

We can graph the Moon’s distance and its angular position.

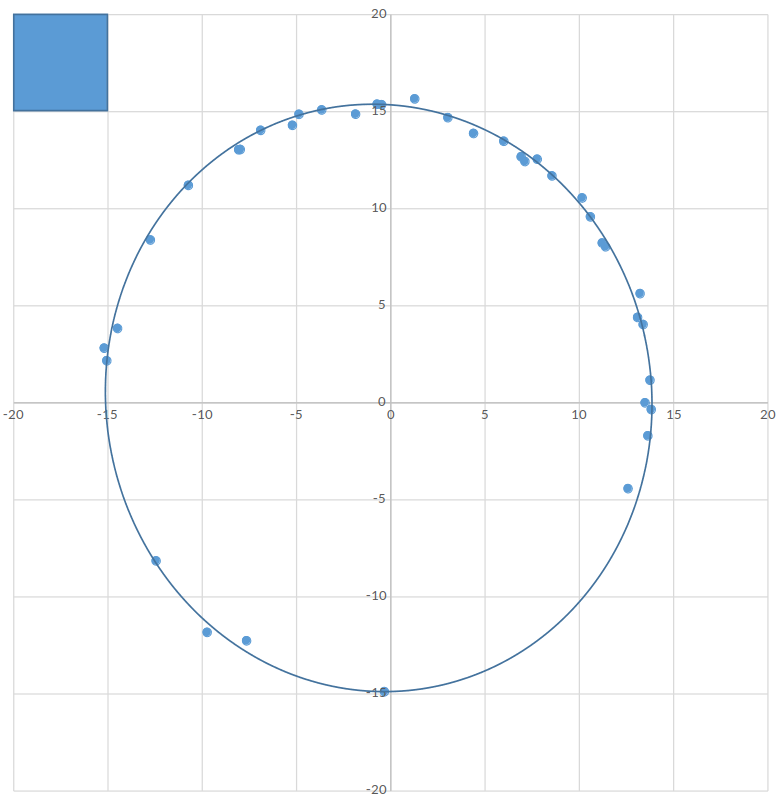
And tadaaaa! We get an ellipse.

We can then measure the smallest and largest distance between the ellipse and the origin (the Earth) to get respectively \(a\), the apogee’s distance, and \(p\), the perigee’s distance.

Using this simple equation, we can get the eccentricity of the Moon’s orbit.

\[e=\frac{a-p}{a+p}\]

And there you go, you have computed the eccentricity of Moon’s orbit just using a camera.

As stated at the start, this experiment blew my mind when I took the course: we calculated the eccentricity of a big rock moving around the Earth just using a camera.

Wow.